English 
Support-Vektor-Maschinen
Eine Linie L zerlegt eine Ebene E in zwei Teile; L heißt dann Hyperebene von E. Eine Ebene E zerlegt einen Raum R in zwei Teile; E heißt dann Hyperebene von R usw. Wenn es möglich ist, zwei Punktmengen in einem Raum durch eine Hyperebene zu trennen, spricht man von der linearen Trennbarkeit eines Problems.
Die Grundaufgabe besteht darin, dass zwei unterschiedliche Klassen von Elementen vorliegen und für ein neues Element entschieden werden muss, welcher Klasse es angehört. Z.B. möchten Banken schon vor der Kreditvergabe gute von schlechten Krediten unterscheiden können und haben größtes Interesse daran zu wissen, wie man solche Kredite bestmöglich erkennen und klassifizieren kann.
Ausgangsbasis für den Bau einer Support-Vektor-Maschine ist ein Trainingskollektiv von Elementen, für welche jeweils bekannt ist, welcher Klasse sie angehören. Dieses Wissen liegt im Falle der Klassifikation von Krediten in Form guter und schlechter Kredite vor, die in der Vergangenheit vergeben wurden. Dieses und ähnliche Probleme sind i.a. nicht linear trennbar, so dass lineare Klassifikatoren für diese Zwecke ungeeignet sind. Hier können sogenannte Support-Vektor-Maschinen eingesetzt werden.
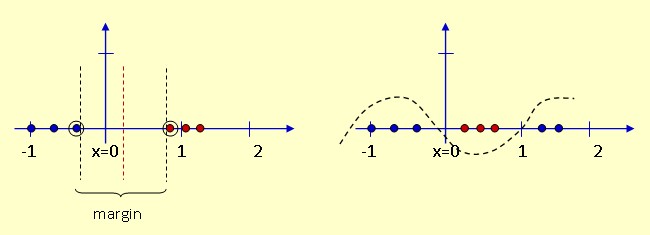
Support-Vektor-Maschinen sind aus der statistischen Lerntheorie hervorgegangen und gehören zum Gebiet des maschinellen Lernens. Sie werden besonders dann eingesetzt, wenn viele Merkmale vorliegen wie etwa bei Krediten. Aufgabe der Support-Vektor-Maschine ist es nun, in den Merkmalsraum eine Hyperebene einzupassen, die als Trennfläche fungiert und die Trainingsobjekte richtig klassifiziert. Der Abstand derjenigen Vektoren, die der Hyperebene am nächsten liegen, - das sind die Stützvektoren - wird dabei maximiert. Der breite Rand (large margin) soll dafür sorgen, dass später Objekte, die sich natürlich von den Trainingsobjekten - z.B. in Form neuer Kreditanträge - unterscheiden, möglichst zuverlässig klassifiziert werden. Im Beispiel unten (s. Abb. links) ist die Trennung der blauen und roten Punktmengen problemlos möglich; es ergibt sich ein breiter Rand (margin). Im rechten Beispiel ist dies nicht möglich. Dazu müßte die Hyperebene sozusagen verbogen werden.
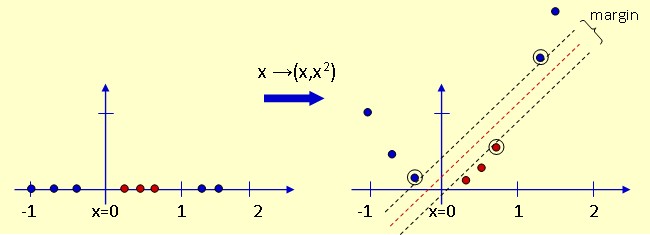
Support-Vektor-Maschinen verwenden hier einen Trick, den sog. Kernel-Trick. Da die Hyperebenen nicht verbogen werden können, werden eben die Punktmengen in geeigneter Weise auseinandergezogen. Hierzu wird durch eine geeignete Kernel-Funktion das Problem nichtlinear in einen hochdimensionalen Raum transformiert, in dem dann eine lineare Separation erfolgen kann. Anschließend erfolgt die Rücktransformation in den Merkmalsraum, und man erhält eine - u.U. sehr komplexe - nichtlineare Trennfläche. Die folgende Abbildung veranschaulicht den Vorgang an einem kleinen Beispiel. Eine einfache Transformation in den zweidimensionalen Raum mittels einer geeigneten Kernel-Funktion löst das Problem sehr elegant. Die umrandeten Punkte stellen dabei wieder die Stützvektoren dar.
